
टाइलिंग या पच्चीकारी उसे कहते हैं जब एक आकृति या आकृतियों के एक समूह को किसी समतल सतह पर इस तरीके से दोहराया या बिछाया जा सके कि कहीं खाली जगह न बचे और न ही आकृतियां एक के ऊपर चढ़ें, और इस बिसात को उस समतल सतह की चारों दिशाओं में अनंत तक आगे बढ़ाया जा सके। आम तौर पर इस तरह की पच्चीकारी में किसी पैटर्न का दोहराव होता है। जैसे कि आपको फुटपाथ पर बिछाई गई फर्शियों, इमारतों की नक्काशियों/जालियों, कपड़ों, मधुमक्खी के छत्ते वगैरह में दिखता है।
लेकिन वर्षों से वैज्ञानिक ऐसी आकृति की तलाश में थे जिससे अनंत तक टाइलिंग की जा सके और उसमें कोई दोहराव वाला पैटर्न न मिले। अब गणितज्ञों को एक ऐसी ही एक वास्तविक आकृति मिल गई है जो बिना दोहराव वाला पैटर्न (एपीरियोडिक टाइलिंग) दे सकती है।
1960 के दशक में पहली बार 20,426 तरह की टाइल इस्तेमाल करके एपीरियोडिक टाइलिंग की गई थी। तब से लगातार इस दिशा में काम होता रहा और एपीरियोडिक टाइलिंग देने वाली एकल आकृति खोजने की कोशिश जारी रही।
इसी प्रयास में नोबेल विजेता गणितज्ञ रॉजर पेनरोज़ ने दो ऐसी अलग-अलग आकृतियां तलाश ली थीं जो मिलकर एपीरियोडिक टाइलिंग कर सकती थीं।
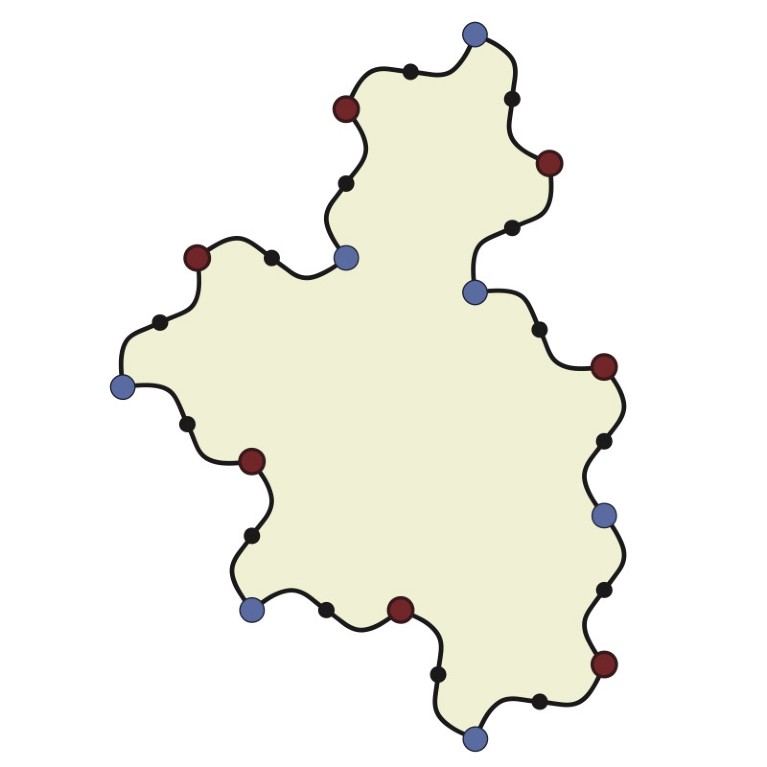
हाल में, ब्रिडलिंगटन (यू.के) के एक शौकिया गणितज्ञ डेविड स्मिथ ने ऐसी ही आकृति की खोज की है। तीन पेशेवर गणितज्ञों के साथ मिलकर उन्होंने दिखाया कि यह आकृति और इसका दर्पण प्रतिबिम्ब अनंत तक एपीरियोडिक टाइलिंग दे सकती है (अभी प्रमाण की समकक्ष समीक्षा बाकी है।)
अब, गणितज्ञों के इसी समूह ने अपनी मूल टाइल में कुछ संशोधन करके एक ऐसी आकृति हासिल कर ली है जो अकेली ही अनंत तक एपीरियोडिक टाइलिंग कर सकती है। इसके प्रमाण आर्काईव प्रीप्रिंट सर्वर पर उपलब्ध हैं और फिलहाल समकक्ष समीक्षा के मुंतज़िर हैं। (स्रोत फीचर्स)
नोट: स्रोत में छपे लेखों के विचार लेखकों के हैं। एकलव्य का इनसे सहमत होना आवश्यक नहीं है।
Photo Credit : https://images.nature.com/original/magazine-assets/d41586-023-01801-8/d41586-023-01801-8_25428052.jpg
https://media.nature.com/lw767/magazine-assets/d41586-023-01801-8/d41586-023-01801-8_25428058.jpg