गणितज्ञों को जो बातें परेशान करती हैं, वे कई बार बहुत विचित्र होती हैं। जैसे 64 साल पुरानी एक पहेली को ही लें। गणितज्ञों का सवाल था कि क्या हरेक संख्या को तीन संख्याओं के घन के जोड़ के रूप में लिखा जा सकता है। अर्थात, क्या हरेक संख्या k के लिए निम्न समीकरण लिखी जा सकती है:
x3 + y3 + z3 = k
यह सवाल वैसे तो एलेक्ज़ेण्ड्रिया के गणितज्ञ डायोफेंटस ने किया था और उक्त समीकरण को डायोफेंटाइन समीकरण कहते हैं। चुनौती यह है कि 1 से अनंत तक किसी भी संख्या (k) के लिए ऐसी तीन संख्याएं खोजें जो उक्त समीकरण को पूरा करें। जैसे यदि संख्या (k) 8 हो तो उसके लिए एक समीकरण निम्नानुसार होगी:
23 + 13 + (-1)3 = 8
आप देख ही सकते हैं कि x, y और z कोई भी संख्या (धनात्मक या ऋणात्मक) हो सकती है। विभिन्न संख्याओं के लिए खोज करते-करते गणितज्ञों को धीरे-धीरे पता चल गया कि सभी संख्याओं के लिए ऐसी समीकरणें लिखना संभव नहीं है। एक नियम यह पता चला कि यदि किसी संख्या में 9 का भाग देने पर शेष 4 या 5 रहे तो उसके लिए ऐसी समीकरण नहीं बन सकती। इस नियम के आधार पर 100 से कम की 22 संख्याएं बाहर हो जाती हैं। शेष 76 संख्याओं के लिए ऐसी समीकरणें बना ली गई हैं किंतु 2 संख्याओं ने गणितज्ञों को खूब छकाया है – 33 और 42।
अब ब्रिस्टल विश्वविद्यालय के एंड्रयू बुकर ने 33 के लिए समीकरण बना ली है। उन्होंने एक कंप्यूटर सूत्रविधि विकसित की जो इस समीकरण को x, y और z के मान 1016 तक लेकर समीकरण का हल निकाल सकती है। उन्हें उम्मीद नहीं थी कि इसकी मदद से कंप्यूटर उन्हें 33 के लिए ऐसी डायोफेंटाइन समीकरण उपलब्ध करा देगी। कुछ सप्ताह की मेहनत के बाद जो समीकरण उन्हें मिली वह थी:
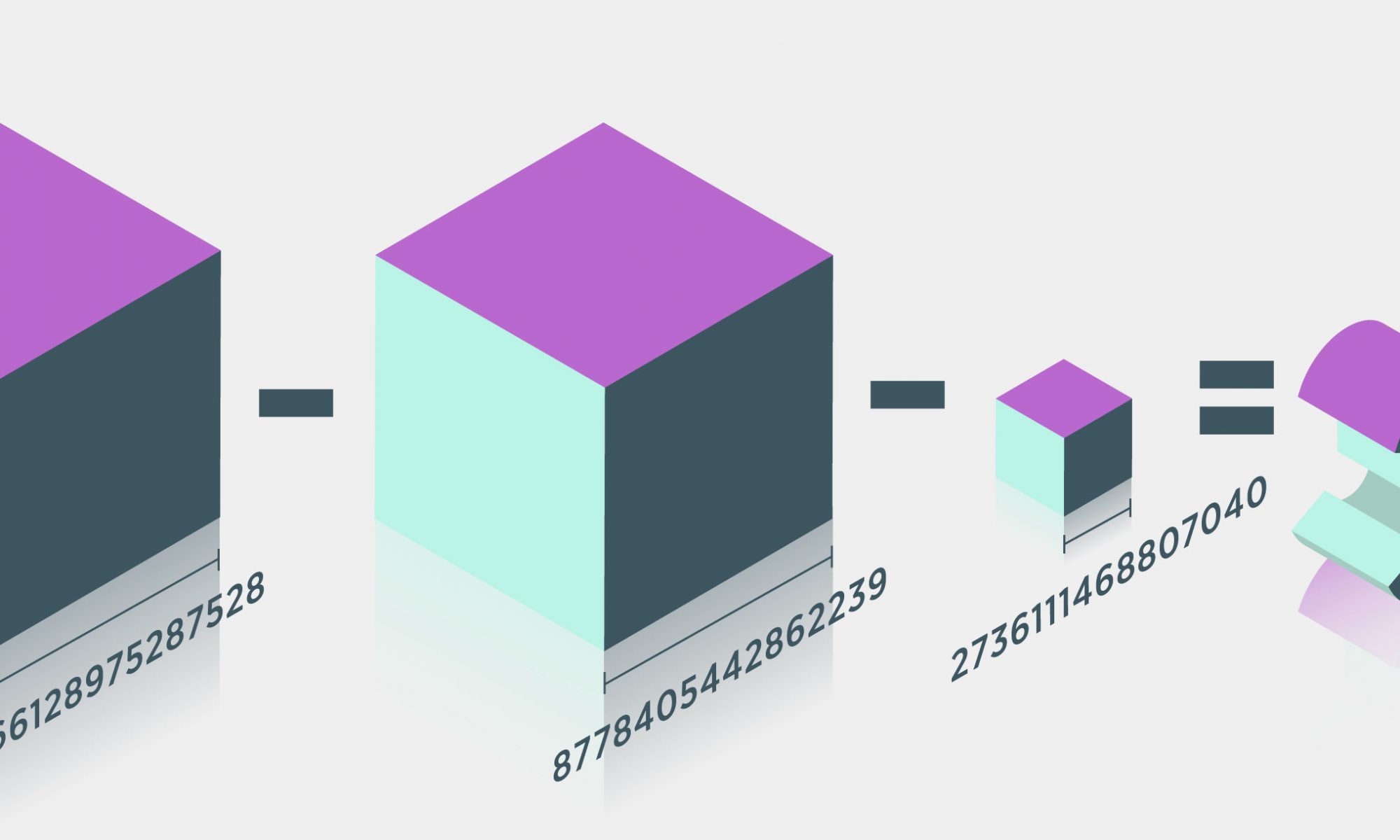
(8,866,128,975,287,528)3 + (-8,778,405,442,862,239)3 + (-2,736,111,468,807,040)3 = 33
बुकर की खुशी का ठिकाना नहीं रहा। मज़ेदार बात यह रही कि उनकी पत्नी को समझ में नहीं आया कि वे इतने खुश क्यों हैं। शायद हममें से भी कई को यह खुशी समझ में नहीं आएगी। मगर 100 से कम की एक संख्या अभी बची है (42) और उम्मीद की जा सकती है कि जल्दी ही कोई और गणितज्ञ खुशी से उछलेगा। (स्रोत फीचर्स)
नोट: स्रोत में छपे लेखों के विचार लेखकों के हैं। एकलव्य का इनसे सहमत होना आवश्यक नहीं है।
Photo Credit : https://d2r55xnwy6nx47.cloudfront.net/uploads/2019/03/Cube33-2880x1220_HP-2880×1220.jpg